ニホンオオカミについてあれこれ調べたり取材して、とても不思議に思ったことがあります。他の動物についての話題に比べると、一般の人々の関心が異常に高いのです(逆に、専門家は話題にもしようとしない)。同じ絶滅動物でもトキの方がこのところ大きな話題にはなっていないのとは対照的です(トキについては新聞などマスコミはよくとりあげていますが、一般に話題になっているとは言い難い)。ニホンオオカミの関心度は謎の動物ツチノコのそれと似ている傾向があると言えるかもしれません。
なぜそんなに関心が強いのか、私には理解できないものがあります。身近な動物にこそ目を向けてほしい、というのが私の信条ですので、いるかいないかもはっきりしない動物に関心が集まるのはとても残念なことです。だからといってこの状況を座視していても仕方ありません。なぜ関心を集めるのか、私なりにいろいろと考えてみました。
まず考えられるのは、絶滅動物だから、という理由です。消え去った(あるいは消え去りつつある)動物に対してのロマンとか罪悪感とか環境問題への意識の高まりとか……いろいろ考えられるでしょう。しかし、そうだとしても同じ絶滅動物であるトキへの関心はそれほどでもありません。国外の絶滅動物、例えばフクロオオカミ(って知ってますか?)への関心はゼロに近いでしょう。
もうひとつ気になったのは、ニホンオオカミについて関心は高くても正確に理解しているわけではないことです。「ニホンオオカミってどんな動物ですか?」と質問してもきちんと答えられる人は皆無でしょう。
こういったことを考えているうちに、私はある考えを思いつきました。[図1]をご覧ください。
三角形のそれぞれの頂点に「一般人(まったく関心を持たない人)」「専門家の見解A」「専門家の見解B」を配置します。そして、これらを結ぶ辺の長さは、意見の隔たりや知識の隔たりを表します。
ニホンオオカミの場合に特徴的なのは、この3辺がどれもとても長く、三角形の面積が大きいということです。一般人と専門家との間の知識の差は当然としても、専門家の間の見解の相違も相当な隔たりがあります。そして、この三角形の中にそれぞれのレベルでのさまざまな見解が存在しているのです。
これがトキの場合になると、専門家の間での意見の相違はほとんどありませんから「専門家の見解A」「専門家の見解B」の距離はとても短いものになります(わからないことは本物を見ればいいことですから論争になりようがありません)。その結果、この三角形の面積は小さくなってしまいます。
三角形が大きいほど話題になりやすいのではないか——というのが私の仮説なのです。
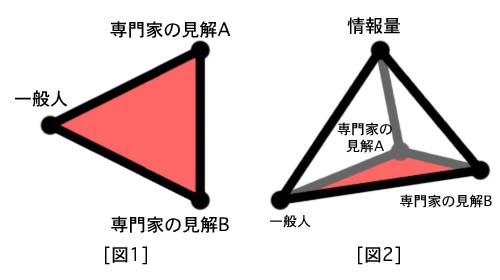
次にツチノコの場合で検証してみましょう。この場合、専門家間の意見の相違はあまりないと思われます。「獲物を飲み込んだヘビ」という見解が普通でしょう。一方で、一般人と専門家との間の知識の差はそれなりにあるでしょう。とはいえ、これではニホンオオカミと比べて三角形の面積は小さいものになるはずです。ということは、他にもパラメーター(変数)がありそうです。うう〜ん、と考えて思いついたのは「情報量」です。この「情報」には不確実な「噂」も含まれます。ツチノコは実物が確認されたことが無いにもかかわらず、毎年のように目撃情報が報告されています。[図1]の三角形に「情報量」を新たに付け加えると[図2]のようになります。この場合は、三角錐の体積が大きいほど話題になりやすいのではないか、という仮説になります。ツチノコはニホンオオカミよりも不確かながらも情報量が格段に多いため、体積も大きくなるのです。
ニホンオオカミに話を戻すと、情報量は少ないながらも底辺の三角形が大きいことが三角錐全体の体積を広げているように見えます。トキの場合は底辺の小ささだけでなく、情報量も多いとはいえないために三角錐の体積が大きくならないのではないでしょうか。
やはり絶滅が確実視されている動物としてフクロオオカミの場合はどうでしょうか。専門家間の意見の相違まではわかりませんし、一般人と専門家との間の知識の差は確かにあるでしょう。ただ、日本にいる限りは情報量は決定的に少量になってしまいます。その結果、体積はとても小さいものになってしまいます。あまり話題にならないわけなのです。
その他の私たちがよく知っている動物、例えばライオン、ペンギン、チンパンジーなどではどうでしょう。これらの動物は情報量はそれなりに多いのですが、そのために専門家間の意見の相違、一般人と専門家との間の知識の差が相対的に小さくなっていると思われます。テレビの動物番組によく登場する動物ならば、一般人でもその暮らしぶりを間近に見ることができるのですから、専門家だけしか知らないということにはなりにくいのです。
というわけで、この「三角錐の体積の大きさは話題の大きさに比例する」という法則ができあがりました。名付けて「ニホンオオカミの三角錐の法則」です(おっと、自分の名前を付けた方が良かったのかな?(笑))。客観的に測定できる法則ではありませんので、まあ軽く読み流してください。とはいえ、世の中の仕組みを理解するヒントにもなりそうな法則にも私には思えてきます。
この法則は逆に応用することも可能でしょう。つまり、話題性を高めるには、(嘘でもいいから)情報をばんばん流せばいいのです。これはマスコミや企業の情報攻勢と似ているところがあるかもしれませんね。
さて、私も動物の話題性を高めるためにこれからもどんどん情報を流さなければなりませんね。あ、でも嘘の情報は流しませんよ。嘘の情報が増えすぎると、その話題がうさんくさくなってしまい、真剣に取り上げられなくなってしまいますからね。